来讨论Oracle收集表字段的唯一值统计使用的算法。11G中对于唯一值(number distinct value NDV)的估算算法,采用的新算法名称为 Approximate NDV。较于10G对于NDV的估算采取快速采样统计法,有了崭新的改进。对于亿级别以上的表数据,新算法无论是估算准确度和所需要的内存空间,都有明显的优势。
Approximate NDV 的算法思想如下:
步骤1. 将扫描到的目标统计列的值通过哈希算法,转换为64位的二进制数(也就是8字节的数字),放入一个叫做概要(synopsis)的数据结构体中。该结构体中包含一个长度为16384的数组和一个level标记。数组的每个单元用来存放转换后的64为二进制值。
步骤2. 扫描下一个列值,转换为哈希64位二进制数,将改二进制数与概要里面已经存在的二进制数做比较。存在相同的则抛弃,否则插入到概要里。
步骤3. 新插入的二进制到概要前,如果发现概要已经满了,则丢弃其中部分数据(具体的做法是,第一次丢弃的时候,丢弃概要里面所有首位为 0 的数值;第二次丢弃的是前面2位为 00 的所有数值;以此类推),我们称之为分裂。每分裂以此,level标识自增1.
步骤4. 扫描到的新哈希值,如果满足丢弃规则,将不再插入概要,直接丢弃。
步骤5. 重复步骤2,3,4的动作,一直到表被扫描完毕。
我们使用 S 表示概要的大小(16384), I 表示级数( level标识,也就是分裂次数), N 表示概要的最终剩余数值数。那么,可以得出一个估算结论:
如果 I=0 则 :
NDV = N
如果 I>0 则 :
NDV = S * 2^I
黄玮在《SQL引擎》中,认为 NDV = S * 2^I 公式里面的 S 表示为概要的最终剩余数值数。我觉得不妥,第一是因为概要的最终剩余值数对于NDV的值的关联系数应该不大,特别是在分裂多次的情况下。第二则是 最终剩余值数不稳定,而从公式上来看,不稳定的S对NDV的影响太大了。
我们从概率论上来理解一下上面的公式:
1)假如我们要计算的是表主键的NDV,那么
NDV= 表的记录数,步骤1 采取的哈希算法分布均匀的理想情况下,步骤2 不会有被丢弃的情况。
概要做第一次分裂的时候,表扫描的记录数为S;这个时候概要会被丢弃 S/2 的记录数(基于哈希算法分布均匀的情况下,首位为 0 和首位为 1 的值数应该是对半开的)。
概要做第二次分裂的时候,表扫描的记录数(不包括第一次分裂之前的记录)为 (1/2) * S * 2^1 .可以理解为:第一次分裂后一直到第二次分裂时,需要插入(1/2) * S 个哈希数到概要里面,从概率上来说,需要扫描 2^1 倍的数量,才可以填满。
以此类推,第三次分裂的时候,表扫描的记录数(不包括第一次分裂之前的记录)为(1/2) * S * 2^2。
第I次分裂的时候,表扫描的记录数(不包括第一次分裂之前的记录)为(1/2) * S * 2^(I-1)
第I次分裂完,一直到扫描结束,这个步骤的表扫描记录数的上限应该为(1/2) * S * 2^I
那么,当NDV统计结束的时候,概要的级数为 I,那么表扫描的记录数为
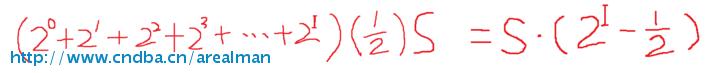
2)假如我们要计算的表普通列,那么结果也是和上面的一致,因为列值相同的列哈希计算后,结果也是相同的。相同的列值在 Approximate NDV 算法步骤2,也会被过滤掉。因此结果的计算公式不变。
由上面的分析过程,其实很容易看出,这个算法的准确性,与哈希算法的质量密切相关,算法离散度越高,分布越均匀,则估算出来的NDV越接近真实。
版权声明:本文为博主原创文章,未经博主允许不得转载。
统计学 NDV 算法




